Heap Sort

Heapsort requires the following operation to get the sorted list. Lets first understand the following operations:

Heapify: Rearrange the remaining elements to maintain the heap property.

Build Max Heap: Construct a max heap from the input array. This involves arranging the elements in the array to satisfy the heap property.

Extract Maximum: Remove the root element (which is the maximum value) from the heap and place it at the end of the array.

Heapify

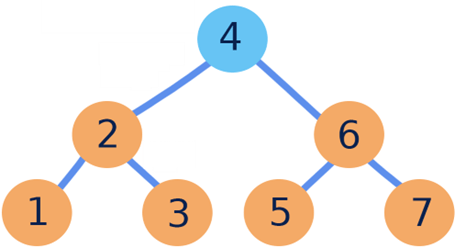
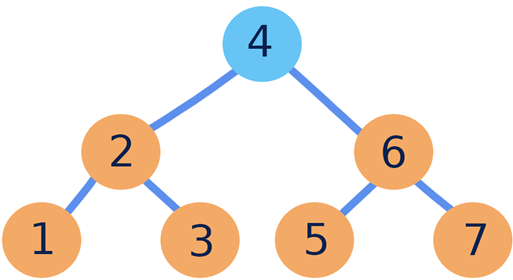
Heapify operation is applied on a node and ensures that this nodes fulfills the structure and order propoerty of heap. Algorithm is as follows

STEPS
index-> 0	1	2	3	4	5	6
4(i)	2(L)	6(R)	1	3	5	7
6		4
		7(i)			(L)	4(R)
6	2	7	1	3	5	7

Build-Max-Heap

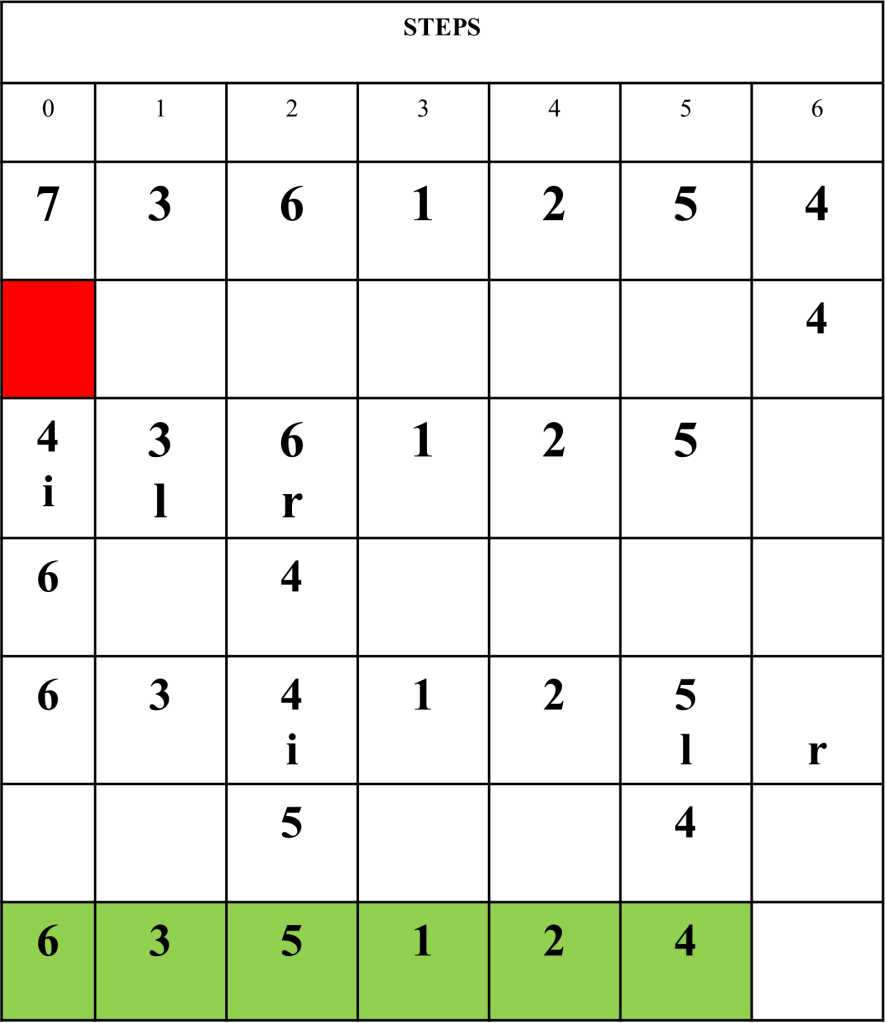
This procedure converts any sequence to a Heap, Basically it applies Max-Heapify operation to all non-leaf nodes as follows

Heap-Extraxt-Max

This operation extracts the maximum element from the Max-Heap, which is the root node of the heap. The logic is to remove the first element and fill this space by last element. The resultant is no more a heap, so Max-heapify (A,0) operation is applied to convert it into heap. The resultant is heap again with size reduces by 1.