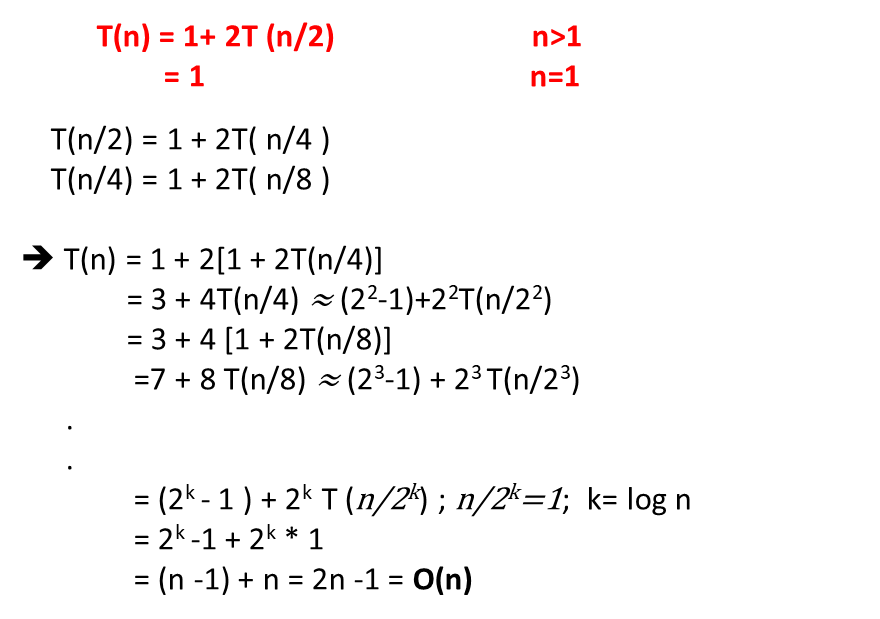Analyzing the running time of a recursive algorithm using the back substitution method involves expressing the time complexity of the algorithm in terms of its recursive calls and then solving the recurrence relation. The back substitution method is a common technique for solving recurrence relations that arise in the analysis of recursive algorithms.
In back substitution method, the goal is to express recurrence relation T(n) in terms of simpler subproblems until you reach a base case. The base case is the smallest instances of the problem for which you know the running time directly. For example, if your algorithm terminates when n = 1, then T(1) is your base case. Lets take an example of solving a recurrence relation using the back substitution method:
Recurrence relation: T(n) = 2 * T(n/2) + O(n)
Base case: T(1) = 1 (assuming the algorithm terminates when n = 1)
Back substitution method solve this recurrence as follows:
- T(n) = 2 * T(n/2) + O(n)
- T(n) = 2 * [2 * T(n/4) + O(n/2)] + O(n)
- T(n) = 2^2 * T(n/2^2) + 2 * O(n/2) + O(n)
- T(n) = 2^3 * T(n/2^3) + 2^2 * O(n/2^2) + 2 * O(n/2) + O(n)
Continue this process until you reach the base case T(1), then simplify and solve the equation to find the time complexity. In this case, it would lead to a time complexity of O(n * log n) for many divide-and-conquer algorithms.
Example -1

Example -2

Example –3

Example – 4

Example -5
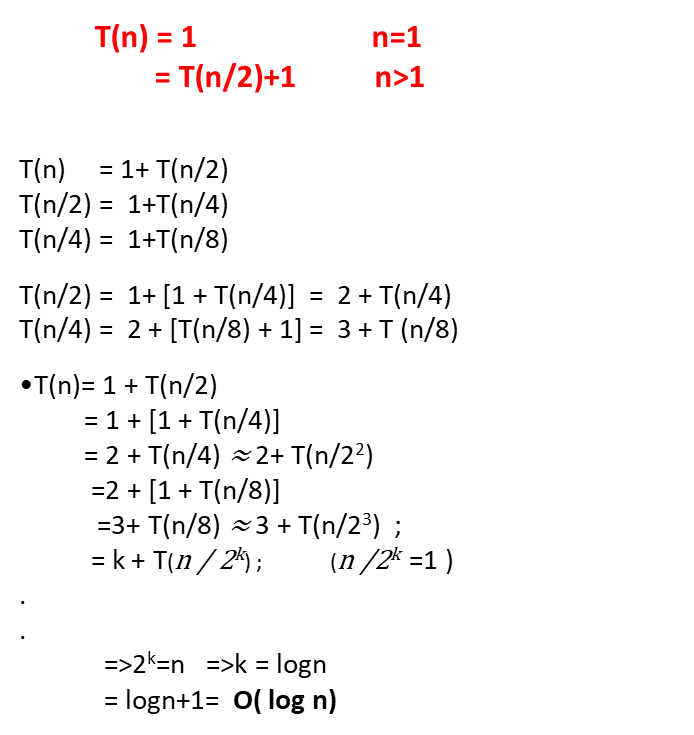
Example – 6

Example -7

Example -8
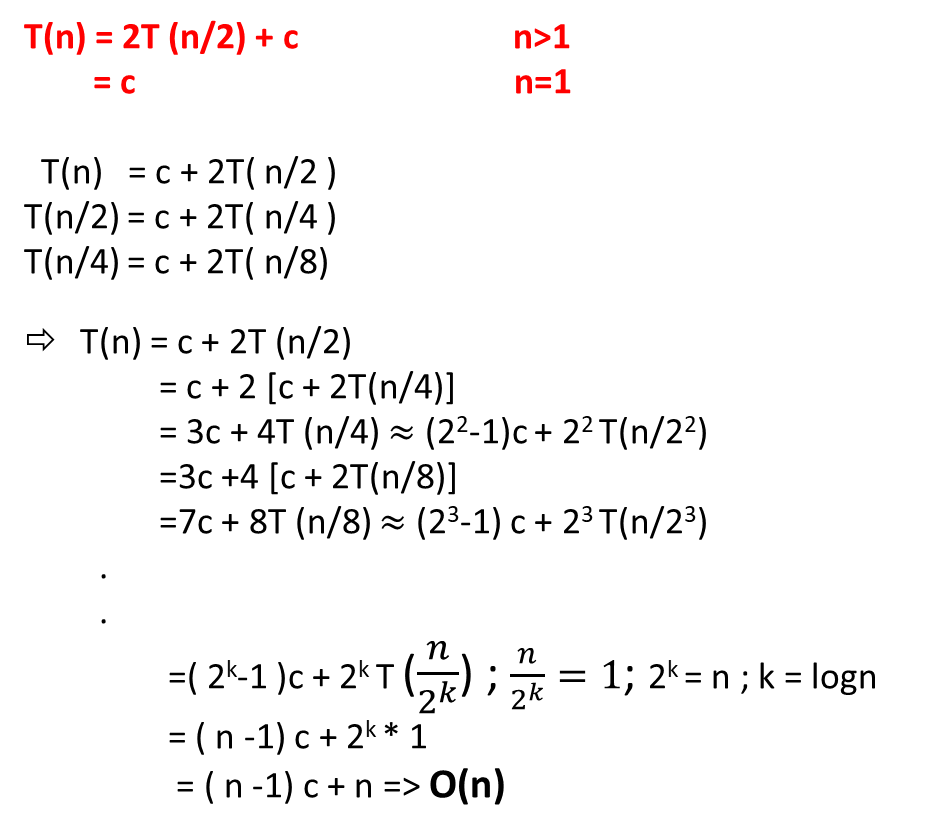
Example -9