Collision resolution techniques are methods used to handle collisions in data structures, particularly in hash tables. A collision occurs in a hash table when two or more keys hash to the same index, causing a conflict in the placement of elements. Effective collision resolution is essential for maintaining the integrity and efficiency of data retrieval operations.
There are several common collision resolution techniques:
- Open hashing / Seperate Chaining
- Closed hasing / Open Addressing
Separate Chaining: In this technique, each bucket in the hash table is implemented as a linked list. When a collision occurs, the colliding elements are simply appended to the linked list at that bucket. Retrieving an element involves scanning the linked list at the corresponding bucket.
Open Addressing: In open addressing, all elements are stored in the table itself. When a collision occurs, the algorithm looks for the next available slot in the table. There are different strategies within open addressing, such as linear probing (move to the next slot), quadratic probing (use a quadratic function to find the next slot), and double hashing (use a second hash function to determine the next slot).
a. Linear Probing: A specific form of open addressing where if a collision occurs, the algorithm looks for the next available slot linearly (one slot at a time). This process continues until an empty slot is found.
b. Quadratic Probing: Similar to linear probing but uses a quadratic function to determine the next probing position. The probing sequence is (hash + 1), (hash + 4), (hash + 9), and so on.
c. Double Hashing: In this method, a secondary hash function is used to determine the step size for probing. If a collision occurs, the algorithm probes with steps determined by the secondary hash function until an empty slot is found.
The choice of collision resolution technique depends on various factors such as the characteristics of the data, the size of the hash table, and the expected pattern of key distribution. Each technique has its advantages and disadvantages, and the efficiency of a hash table can be influenced by the specific use case and the quality of the chosen hash functions.
Example Open hashing / Seperate Chaining
It is one of the most commonly used collision resolution techniques. It is usually implemented using linked lists. In separate chaining, each element of the hash table is a linked list.
- To store an element in the hash table we insert it into a specific linked list.
- If there is any collision (i.e. two different elements have same hash value) then store both the elements in the same linked list.
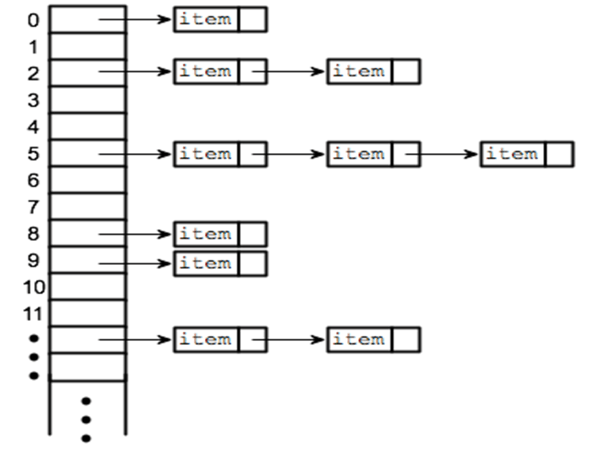
Consider the insertion of elements 5, 28, 19, 15, 20, 33, 12, 17, 10 into a chained-hash-table with 9 slots. The table uses the following hash function h(k) = k mod 9
Soln – elements are inserted as
h(5) = 5 mod 9 = 5 h(28) = 28 mod 9 = 1 h(19) = 19 mod 9 = 1 h(15) = 15 mod 9 = 6
h(20) = 20 mod 9 = 2 h(33) = 33 mod 9 = 6 h(12) = 12 mod 9 = 3 h(17) = 17 mod 9 = 8
Note : Elements are inserted in beginning to keep O(1)
Linear probing (open addressing or closed hashing)
Probing is the process of examining the slots in the hash table
“open addressing” refers to the fact that the location or address of the item is not determined by its hash value.
In open addressing, instead of in linked lists, all entry records are stored in the array itself.
When a new entry has to be inserted
==> the hash index of the hashed value is computed and then the array is examined (starting with the hashed index).
==> If the slot at the hashed index is unoccupied, then the entry record is inserted in slot at the hashed index else it proceeds in some probe sequence until it finds an unoccupied slot.
Probe sequence is the sequence that is followed while traversing through entries.
In different probe sequences, we have different intervals between successive entry slots or probes.
When searching for an entry
==> the array is scanned in the same sequence until either the target element is found or an unused slot is found. unused slot indicates that there is no such key in the table. In Linear probing the interval between successive probes is fixed (usually to 1).
Example Consider inserting the keys 76, 26, 37, 59 into hash table of size m =11 using liner probing .
Use hash function h’(k) = k mod m
Solution : using h(k,i) = [h’(k) + i ] mod m
Key k =76 => h(76,0)= (76 mod 11 + 0)mod 11 = (10 + 0) mod 11 = 10 mod 11 = 10 (empty)
Key k = 26 => h(26,0)= (26 mod 11 + 0)mod 11 = (4 + 0) mod 11 = 4 mod 11 = 4 (empty)
Key k = 37 => h(37,0)= (37 mod 11 + 0)mod 11 = (4 + 0) mod 11 = 4 mod 11 = 4 (occupied)
next probe sequence => h(37,1)= (37 mod 11 + 1)mod 11 = (4 + 1) mod 11 = 5 mod 11 = 5 (empty)
Key k = 59 => h(59,0)= (59 mod 11 + 0)mod 11 = (4 + 0) mod 11 = 4 mod 11 = 4 (occupied)
next probe sequence => h(59,1)= (59 mod 11 + 1)mod 11 = (4 + 1) mod 11 = 5 mod 11 = 5 (occupied)
next probe sequence => h(59,2)= (59 mod 11 + 2)mod 11 = (4 + 2) mod 11 = 6 mod 11 = 6 (empty)
Quadratic probing
Linear probing is easy to implement but it suffers from primary clustering. Cluster means block of occupied slots. Primary clustering refers many such blocks separated by free slots. It increases number of probes to find a free slot
Quadratic probing is similar to linear probing and the only difference is the interval between successive probes or entry slots. Quadratic Probe uses the following hash function
h(k, i) =[h’(k)]+c1i + c2 i2] mod m
Here m is the size of the hash table, h’(k) = k mod m ( hash fns), c1 and c2 are constants not equal 0, i is probe number
In Quadratic probing when the slot at a hashed index for an entry record is already occupied, we start traversing until you find an unoccupied slot.
The interval between slots is computed by adding the successive value of an arbitrary polynomial in the original hashed index.
Example Consider inserting the keys 76, 26, 37, 59 into hash table of size m =11 using quadratic probing . [given c1= 1 and c2=3]
Use hash function h’(k) = k mod m
Solution : using h(k, i) =[h’(k)]+c1i + c2i2] mod m = [ k mod 11 + 1xi + 3x i2] mod 11
Key k =76 => h(76,0)= [ 76 mod 11 + 0 + 3 x 0] mod 11 = (10 + 0 + 0) mod 11 = 10 mod 11 = 10 (empty)
Key k = 26 => h(26,0)= [ 26 mod 11 + 0 + 3 x 0] mod 11 = (4 + 0 + 0) mod 11 = 4 mod 11 = 4 (empty)
Key k = 37 => h(37,0)= [ 37 mod 11 + 0 + 3 x 0] mod 11 = (4 + 0 + 0) mod 11 = 4 mod 11 = 4 (occupied)
next probe sequence => h(37,1) = [ 37 mod 11 + 1 + 3 x 1] mod 11 = (4 + 1 + 3) mod 11 = 8 mod 11 = 8 (empty)
Key k = 59 => h(59,0) = [ 59 mod 11 + 0 + 3 x 0] mod 11 = (4 + 0 + 0) mod 11 = 4 mod 11 = 4 (occupied)
next probe sequence => h(59,1) = [ 59 mod 11 + 1 + 3 x 1] mod 11 = (4 + 1 + 3) mod 11 = 8 mod 11 = 8 (occupied)
next probe sequence => h(59,2) = [ 59 mod 11 + 2 + 3 x 4] mod 11 = (4 + 2 + 12) mod 11 = 18 mod 11 = 7 (empty)
Double hashing
Double hashing is similar to linear probing and the only difference is the interval between successive probes. Here, the interval between probes is computed by using two hash functions. Lets linear probing uses the following hash function h(k,i) = [h1(k) + i.h2(k) ] mod m
Here m is the size of the hash table, h1(k) = k mod m ( hash fns), h2(k) = k mod m’ [hash fns with slightly less m (say m-1)], i is 0 to m-1
Example Consider inserting the keys 76, 26, 37, 59 into hash table of size m =11 using double hashing.
Use hash function h1(k) = k mod 11 and h2(k) = k mod 9
Solution : using h(k,i) = [h1(k) + i.h2(k) ] mod m
Key k =76 => h1(76)= (76 mod 11) =10 and h2(76) = 76 mod 9 = 4
h(76,0) = (10 + 0 x 4 ) mod 11 = 10 mod 11 = 10 (empty)
Key k = 26 => h1(26)= (26 mod 11) =4 and h2(26) = 26 mod 9 = 8
h(26,0) = (4 + 0 x 8 ) mod 11 = 4 mod 11 = 4 (empty)
Key k = 37 => h1(37)= (37 mod 11) =4 and h2(37) = 37 mod 9 = 1
h(37,0) = (4 + 0 x 1 ) mod 11 = 4 mod 11 = 4 (occupied)
next probe sequence => h(37,1) = (4 + 1 x1 ) mod 11 = 5 mod 11 =5 (empty)