Practise Numericals

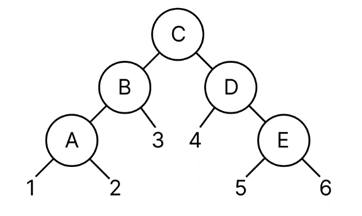
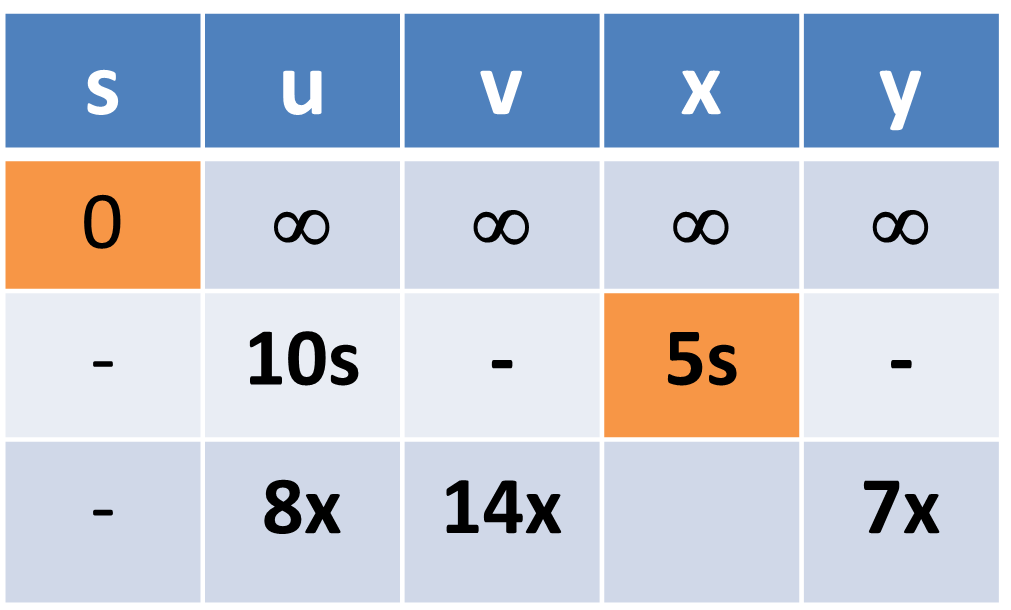Here are few examples that will help you to prepare for any Computer Algorithms Examination

Asymptotic Notations (Big-oh, Omega, Theta)
Solving Recurrence Equations (using recurrence tree & back-substitution)
Solving Recurrences using Masters theorem
Solving Heap Based Problems (heapify, build-heap, extract-max)
Sorting Based Problems (quick-sort, merge-sort, heap-sort, radix-sort)
Red Black Tree Operations
Order Statistics Tree & Interval Tree Operations (rank, k-th smallest)
Splay Tree Operations
Finding Minimum Spanning Tree (MST) (using Prims and Kruskal)
FInding Shortest Path (using Djikshtra and Bellman Fords)
Problem Solving using Greedy Approach (solving 0/1 and Fractional Knapsack)
Problem Solving using Dynamic Programming
Finding Pattern in Given String (using KMP and Boyers- Moore Algorithms)

Problems on Asymptotic Notations

Question : Find the O- notation for following functions. (Show the steps to evaluate value of c and n_o)

Solution : (click for video explanation)

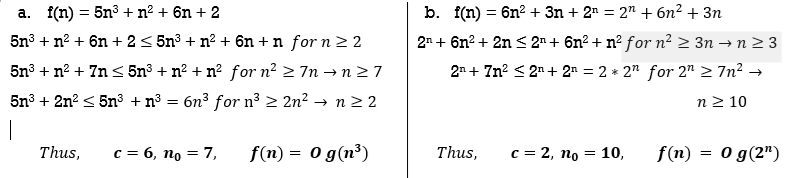
Question : Find the big omega- notation for following functions. (Show the steps)

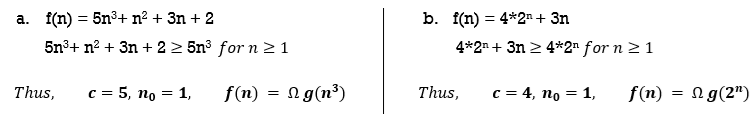
Question : Find the theta notation for following functions. (Show the steps)

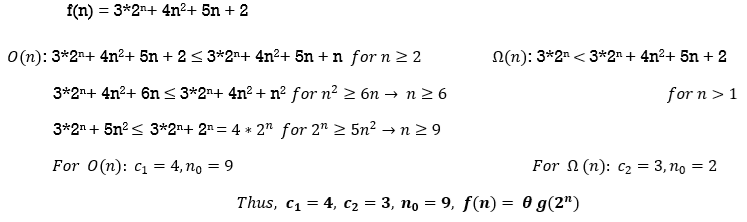
Question : Comment on the following (check bounds are correct or incorrect)

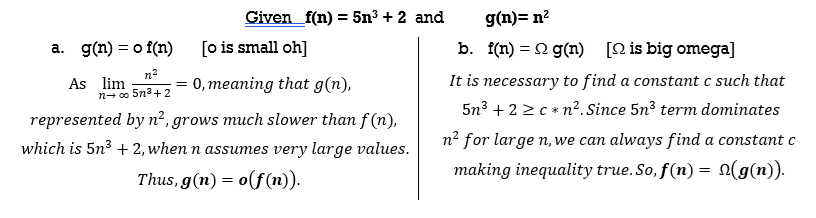
Problem on Recurrence Equations

Question : Solve following Recurrence using Back Substitution method

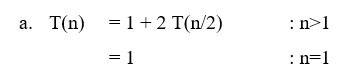
Solution : ( click for video explanation)

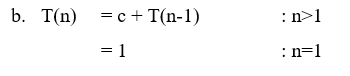
Solution : ( click for video explanation)

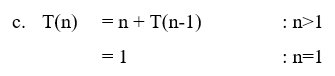
Solution :

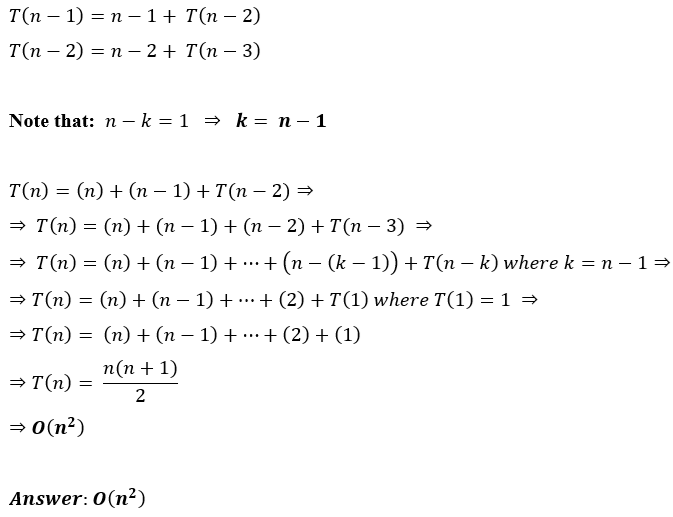
Question : : Solve following Recurrence using Recursive Tree method

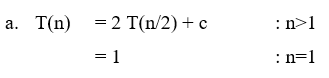
Solution : ( click for video explanation )

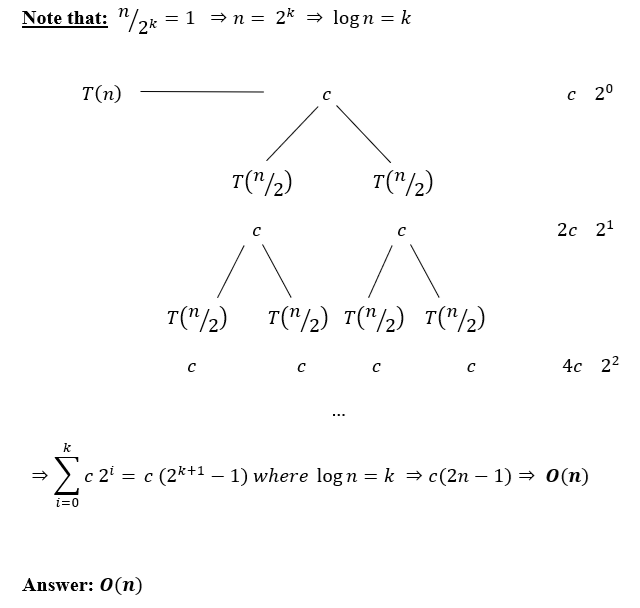
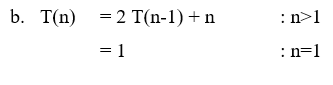
Solution : ( click for video explanation )

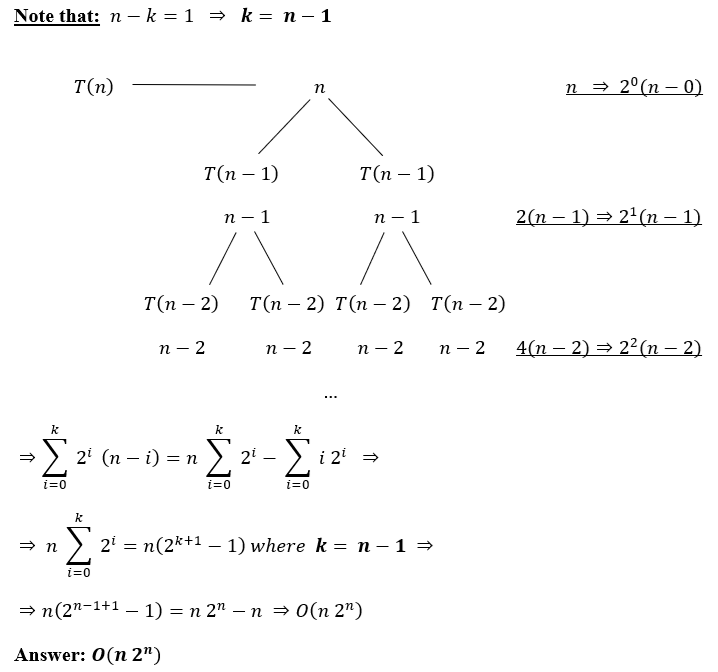
Probelms on Master’s Theorem

Question : Solving following Recurrence Equations using Masters Theorem

Solution : ( click for video explanation )

Problem on Heap

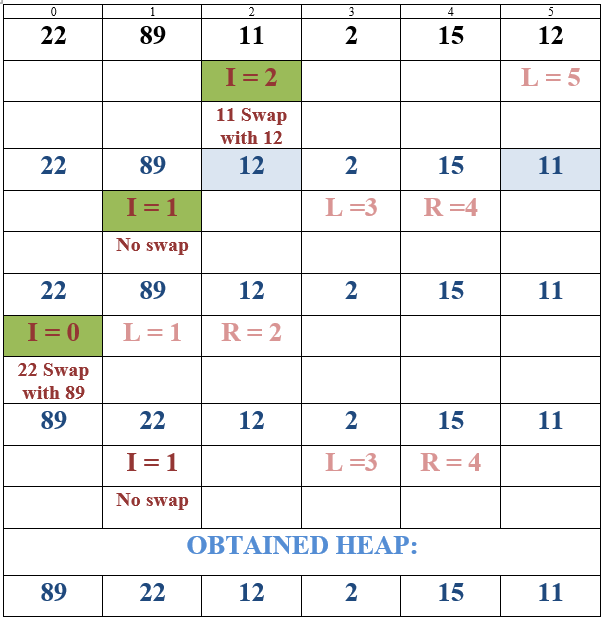
Question : Convert the following sequence to a Heap using Build Max Heap

22, 89, 11, 2, 15, 12

Solution : ( click for video explanation )

Execution STEPS

A = [22, 89, 11, 2, 15, 12]

Length(A) = 6

MAX-HEAPIFY(A, 2) l = 5, r = 6 r does not exist. A[2] change with A[5].
MAX-HEAPIFY(A, 1) l = 3, r = 4, nothing happens.
MAX-HEAPIFY(A, 0) l = 1, r = 2, A[0] change with A[1].

MAX-HEAPIFY(A, 1) l = 3, r = 4, nothing happens.

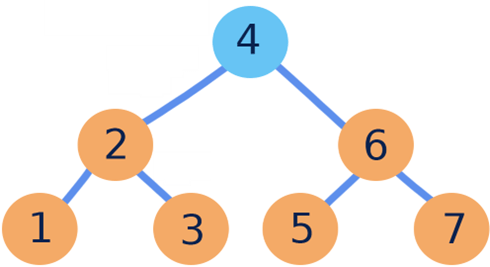
Question : Apply Build-Max-Heap on following tree

Question: Apply Max-Heapify (A,0) on following tree

STEPS
0	1	2	3	4	5	6
4	2	6	1	3	5	7
6		4
		7				4
6	2	7	1	3	5	7

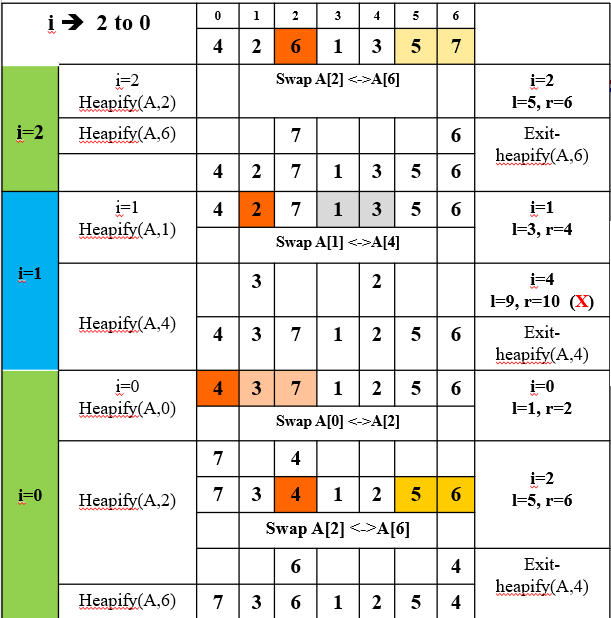
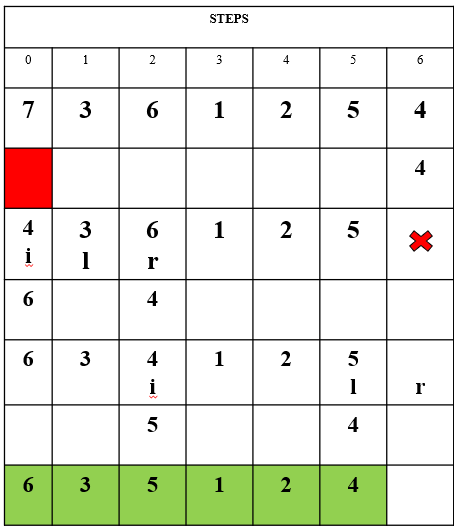
Question: Apply Heap-Extract-Max in the following heap

0	1	2	3	4	5	6
7	3	6	1	2	5	4

Solution

Problems on Sorting

Question : Apply Quicksort Algorithm to sort the given sequence

7 18 19 43 12 5 26

Solution ( click for video explanation )

Following steps show only steps of PARTITION on the initial array

Question : Apply Merge sort Algorithm to sort the given sequence

11 16 29 4 2 15 6

Solution : ( click for video explanation )

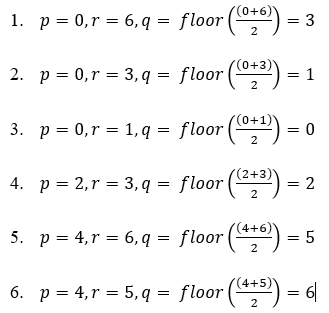
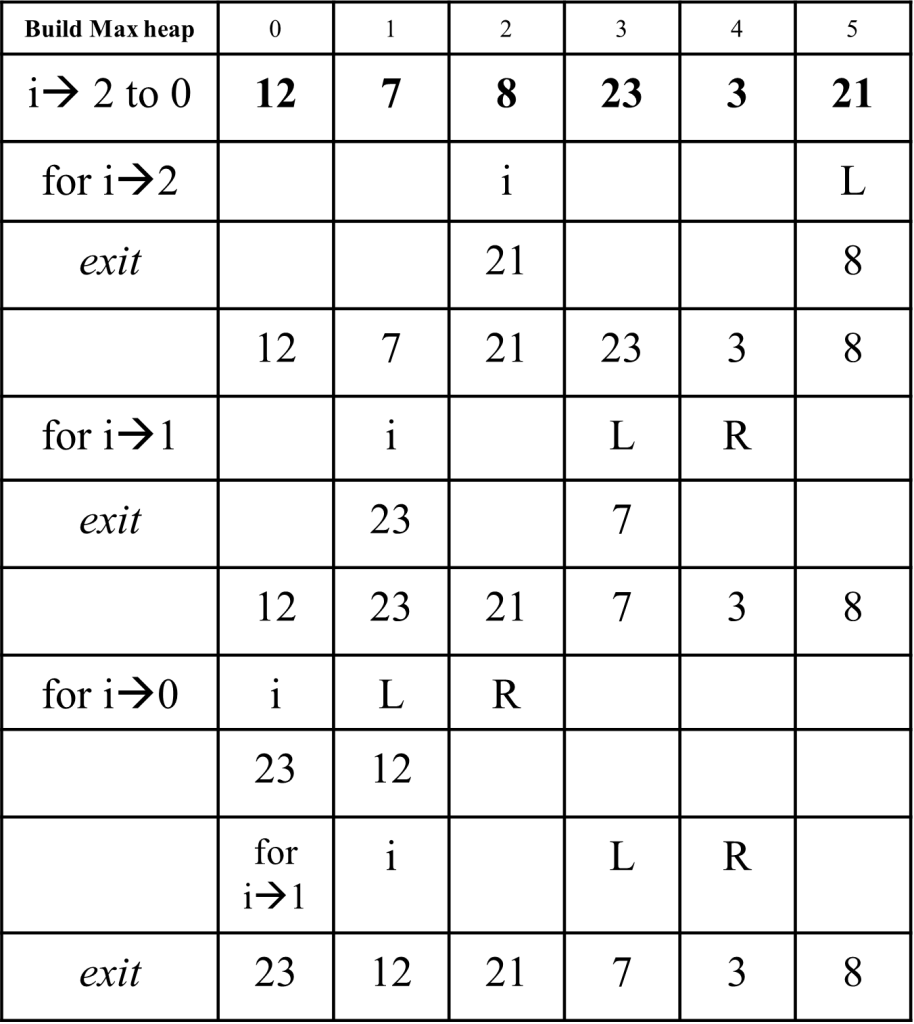
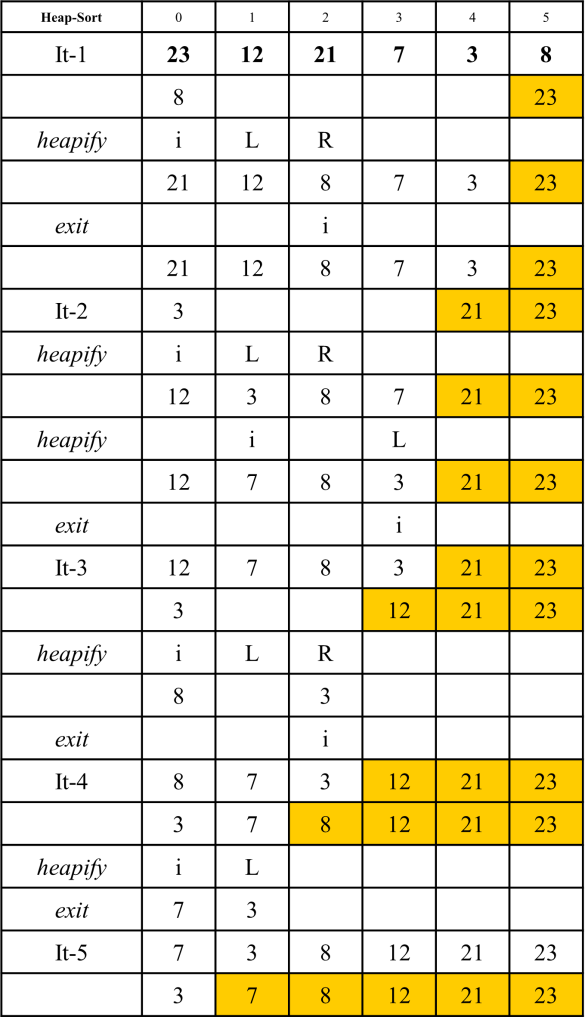
Question : Apply Heap sort Algorithm to sort the given sequence

12, 7, 8, 23, 3, 21

Solution : (click for video explanation)

Heap Sort requires the given sequence to be converted to heap, then the sorting is applied. Following are the algorithm used

Steps for converting Heap and then Heap-sort is shown below

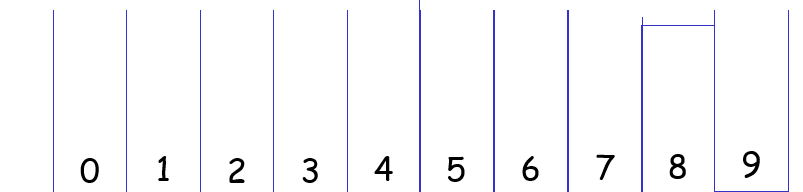
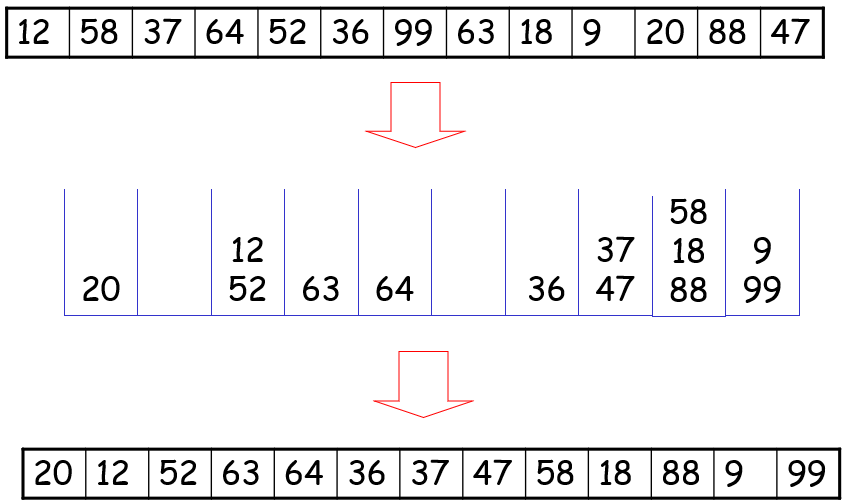
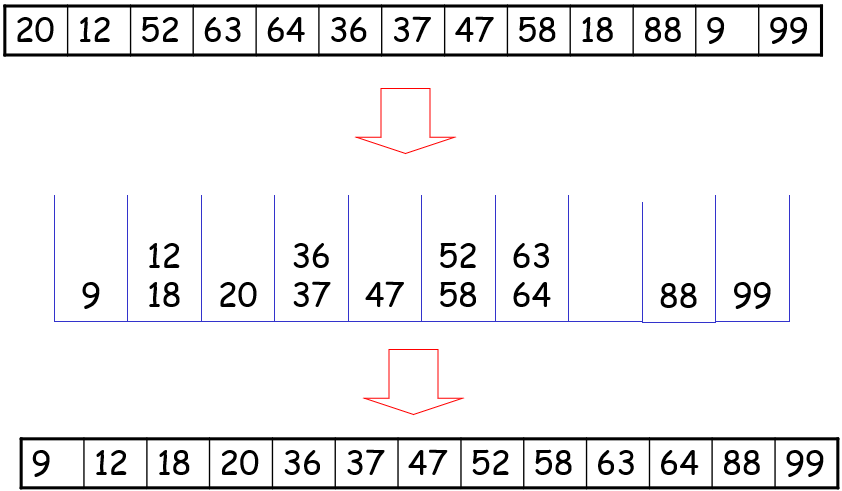
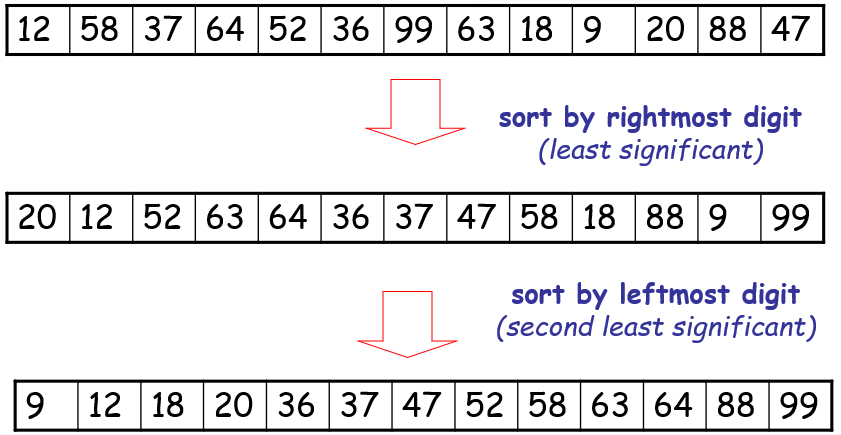
Question : Apply Radix sort Algorithm to sort the given sequence

12, 58, 37, 64, 52, 36, 99, 63, 18, 9, 20, 88, 47

Solution: (click for video explantion)

Since all data elements are integers, 10 buckets are required numbered 0-9 as follows, buckets are empty initially.

The entire process requires two passes as maximum number in the sequence consist of 2 digits.

First pass is as follows

Second Pass is as follows

Therefore, the sorted sequence is achieved by undergoing passes as follows

Problems on Red Black (RB) tree

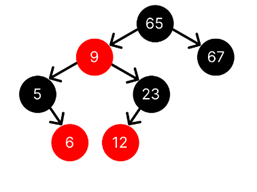
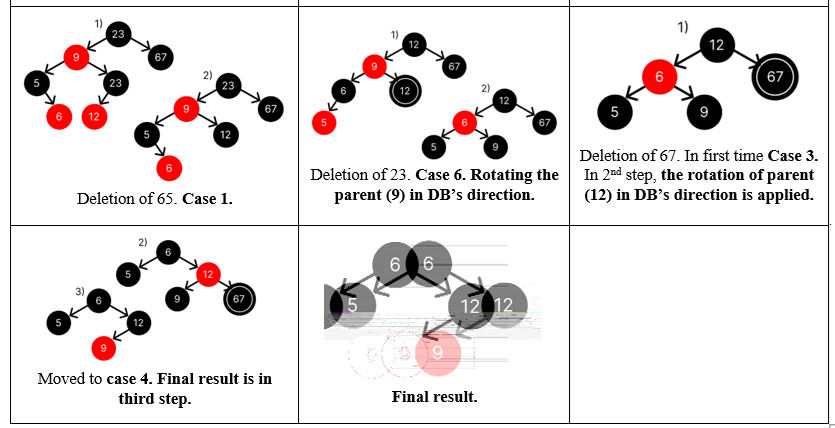
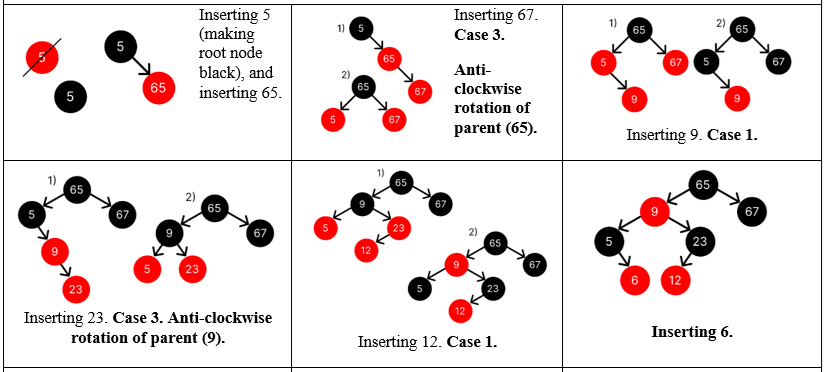
Question : Construct the RB tree by inserting following nodes

5, 65, 67, 9, 23, 12, 6

Solution ( click for video explanation )

Question : Delete from the RB tree following nodes 65, 23, 67

Solution : ( click for video explanation )

Operations on Order Statistic Tree & Intreval Trees

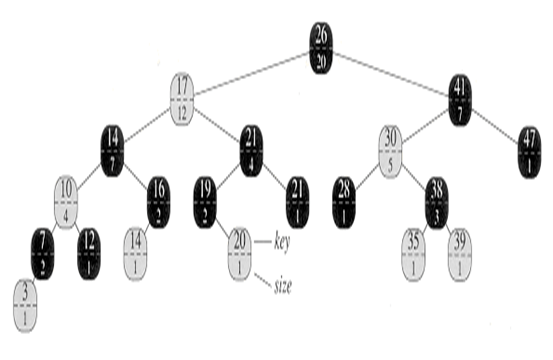
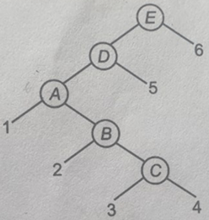
Question : Find the Rank of key 41 and key 38 in the following order-statistics tree

Note : ( click for video explanation )

Rank of Key 41 –Solution as follows

Iteration	Key	r
1	41	6, 19
2	26	19

Answer is 19

Rank of Key 38 –Solution as follows

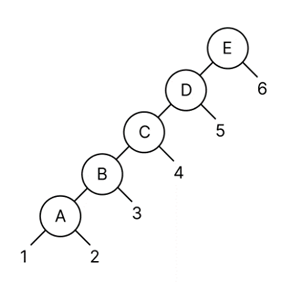
Question : Find the 7th smallest in the following order-statistics tree

Solution – 7^th smallest is found as follows

(click for video explanation)

key	i	r
17	7	8 ( i < r )
14	7	5 ( i > r )
16	2	2 ( i = r )

7th smallest is Key 16

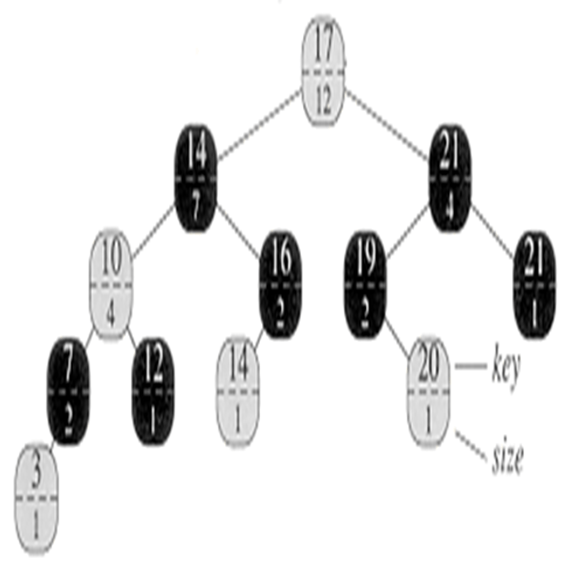
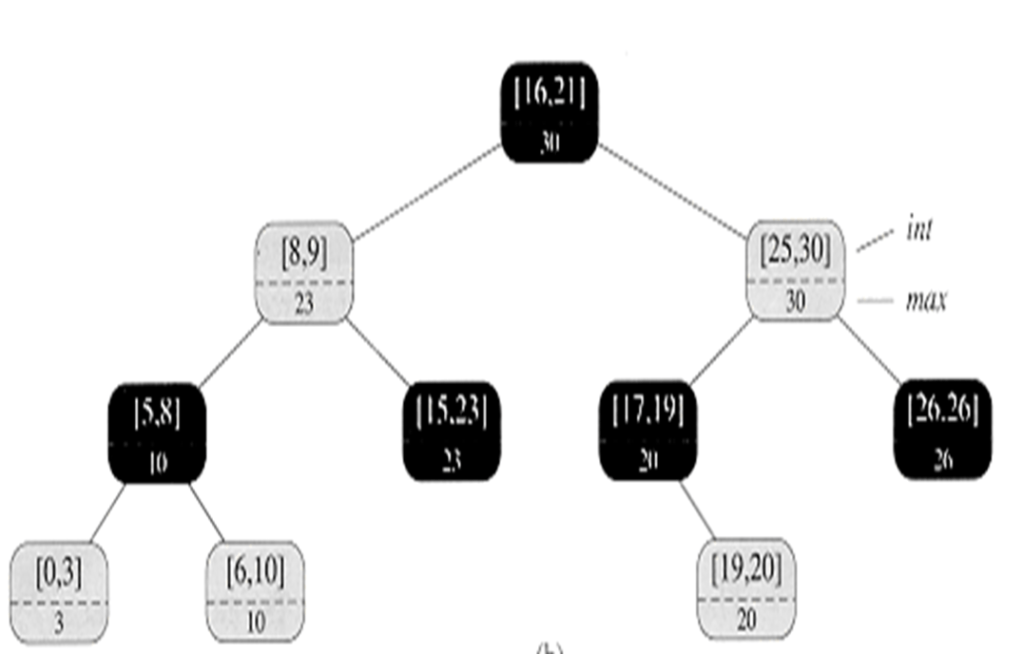
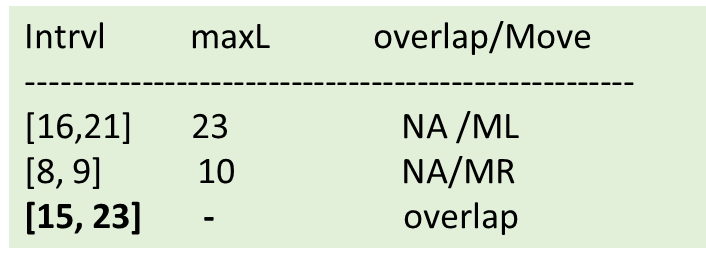
Question : Find the Interval [22, 24] in the following Interval tree

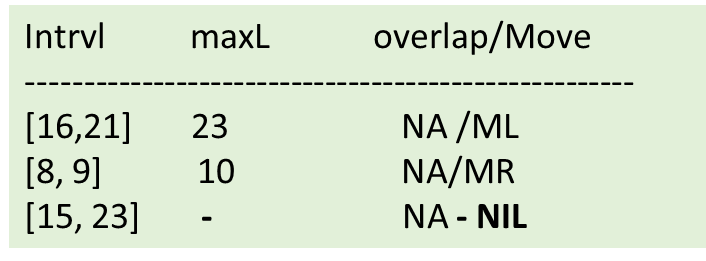
Solution – Using the following algorithm to search for an interval

Question : Find the Interval [11, 44] in the above Interval tree

Explanation (click for video explanation)

Splay Tree Operations

Question : Splay node C in the following tree

Solution : ( click for video explanation )

Question : Splay node A in the following tree

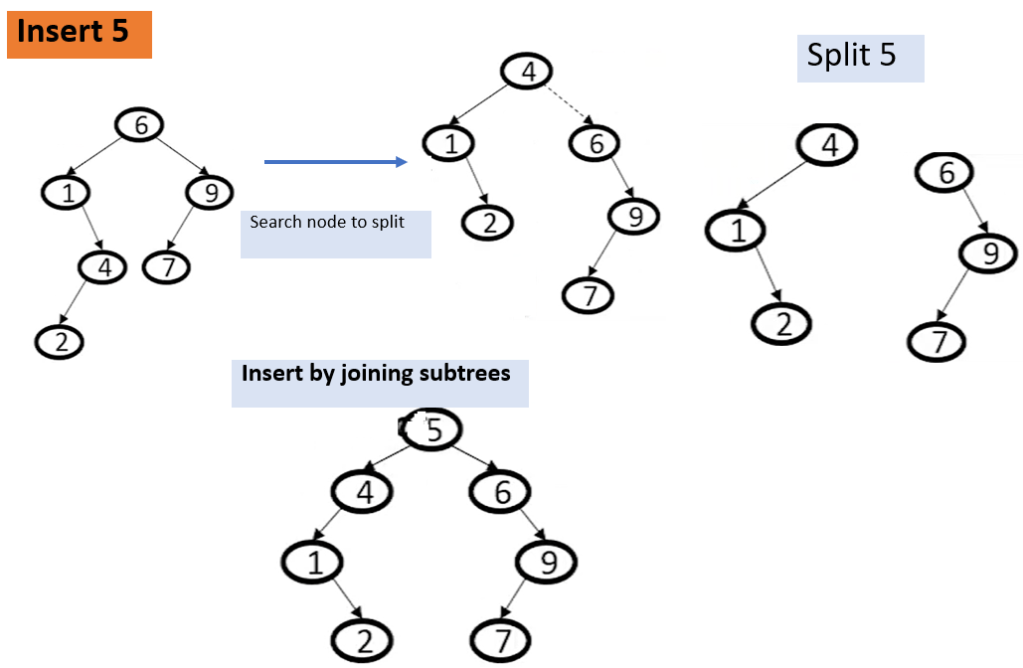
Question : Insert Node with Key value 5 in Splay tree using Split Method (click for video explanation)

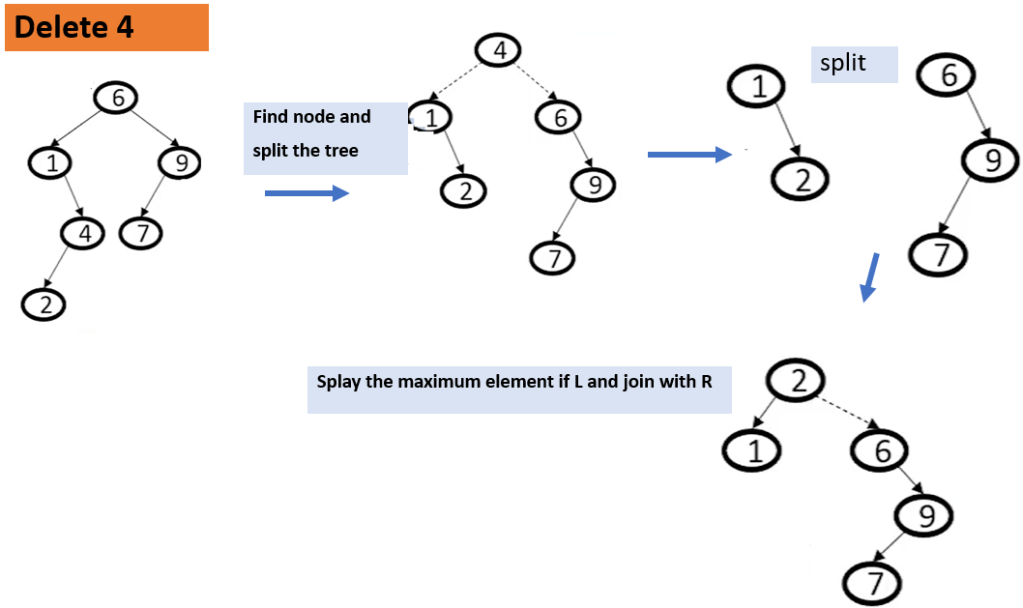
Question : Delete Node with Key value 4 in Splay tree using Split Method click for video explanation)

Problems of Minimum Spanning Tree ( MST )

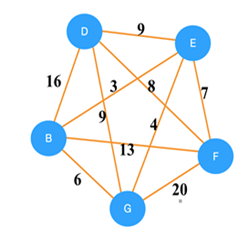
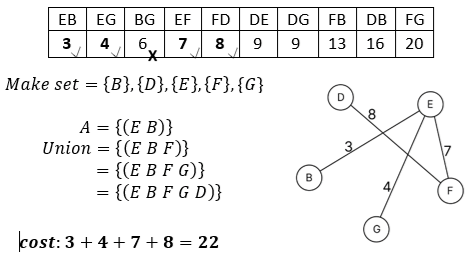
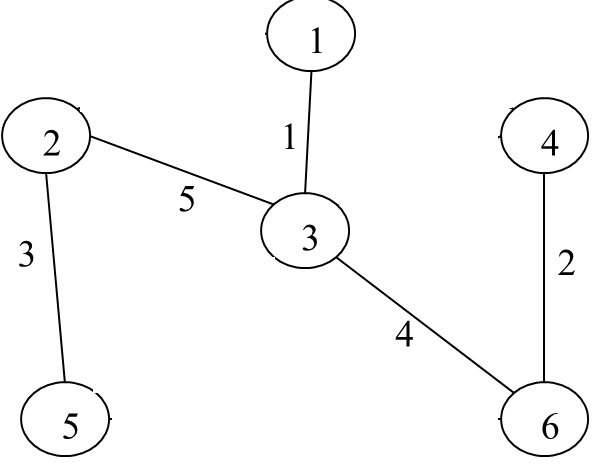
Question : Finding the MST using Krushkal method, also find the cost of MST.

Solution : Detailed steps as follows ( click for video explanation )

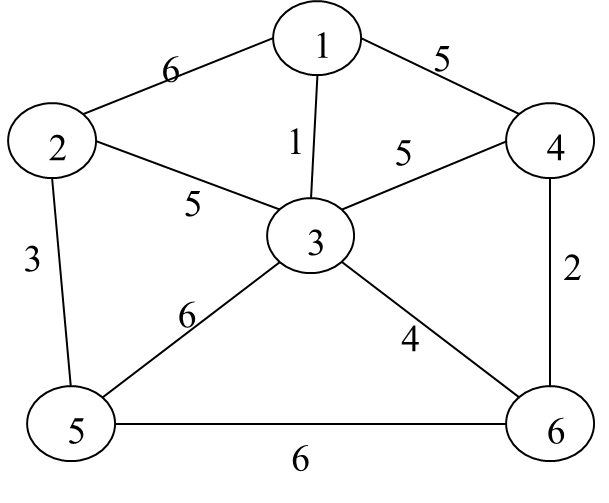
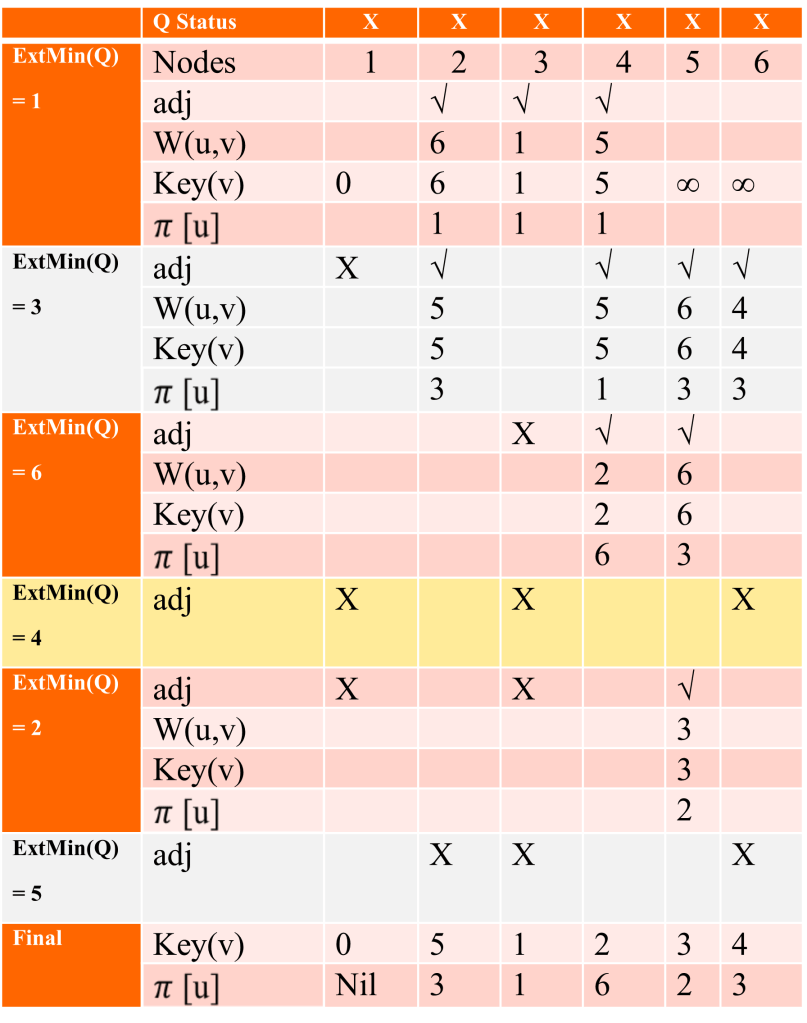
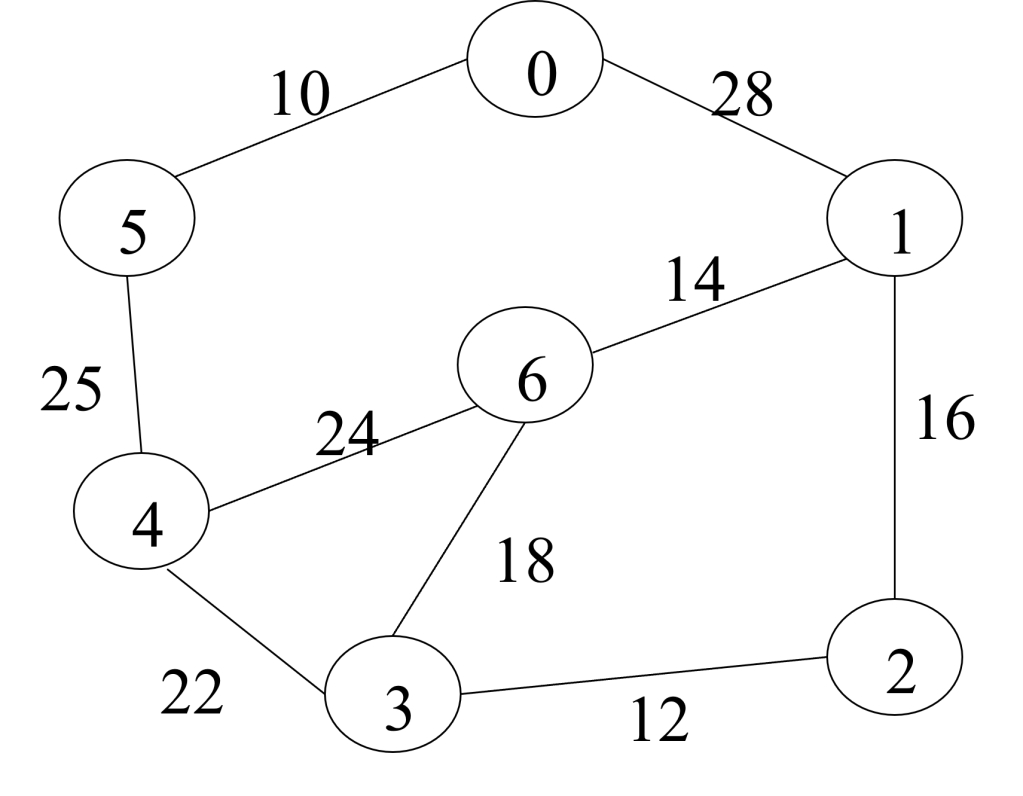
Question : Finding the MST using PRIMs method, also find the cost of MST

Solution : Detailed steps as follows (click for video explanation)

Cost = 3+5+1+4+2 =15

The last row defines predessor of the nodes shown in first row in the table shown

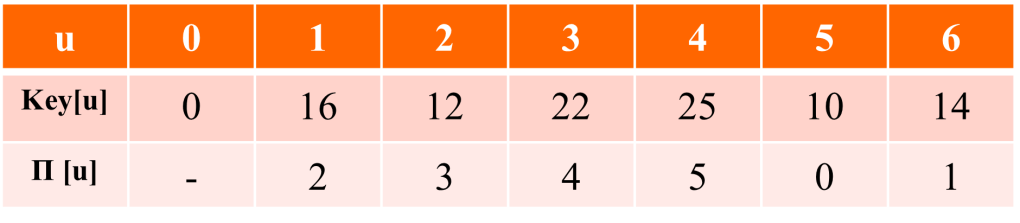
Question : Following information is derived using PRIMs algorithms for the graph , Find the MST

Solution : MST shown as follows (click for video explanation)

Problem on Shortest Path

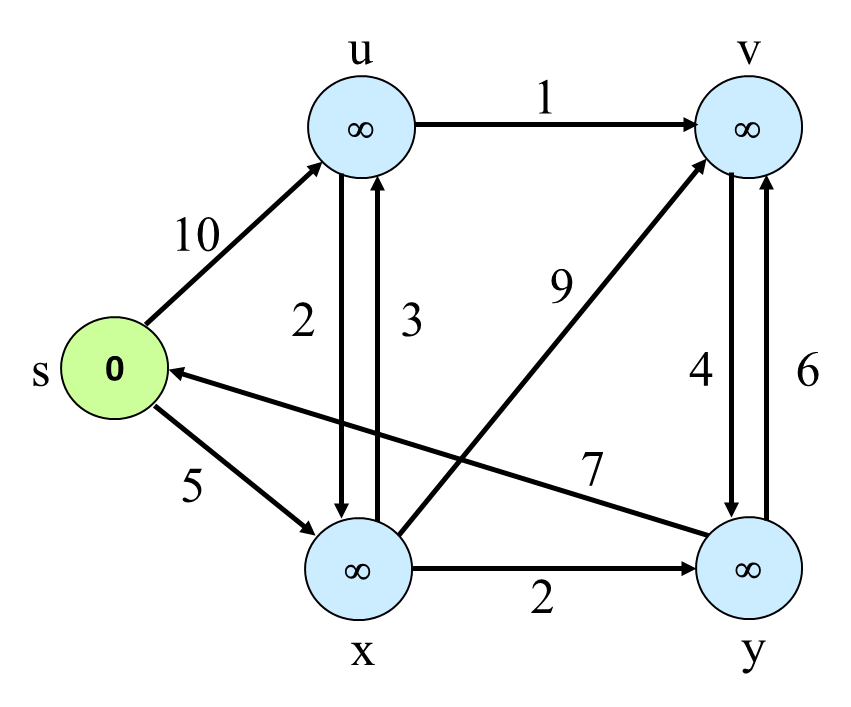
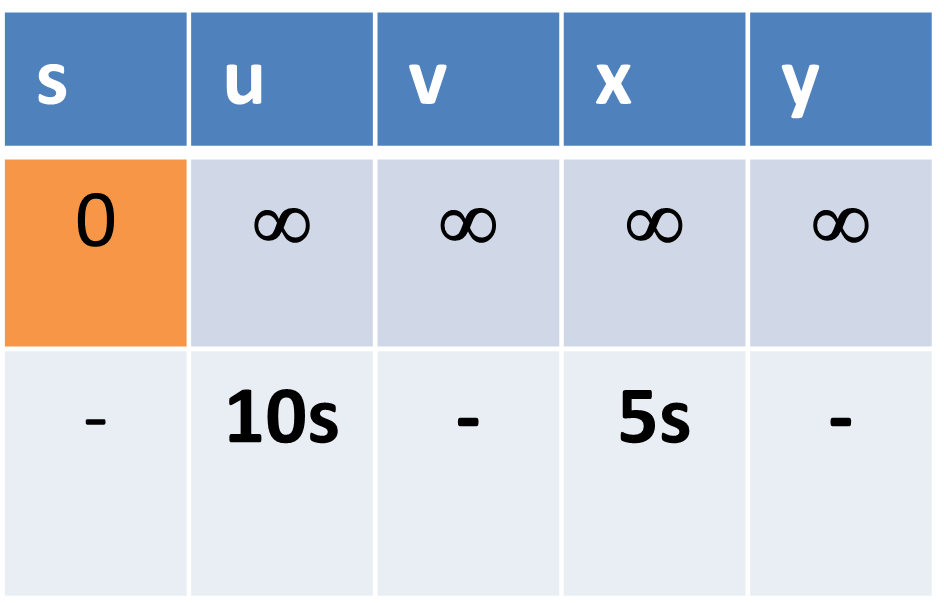
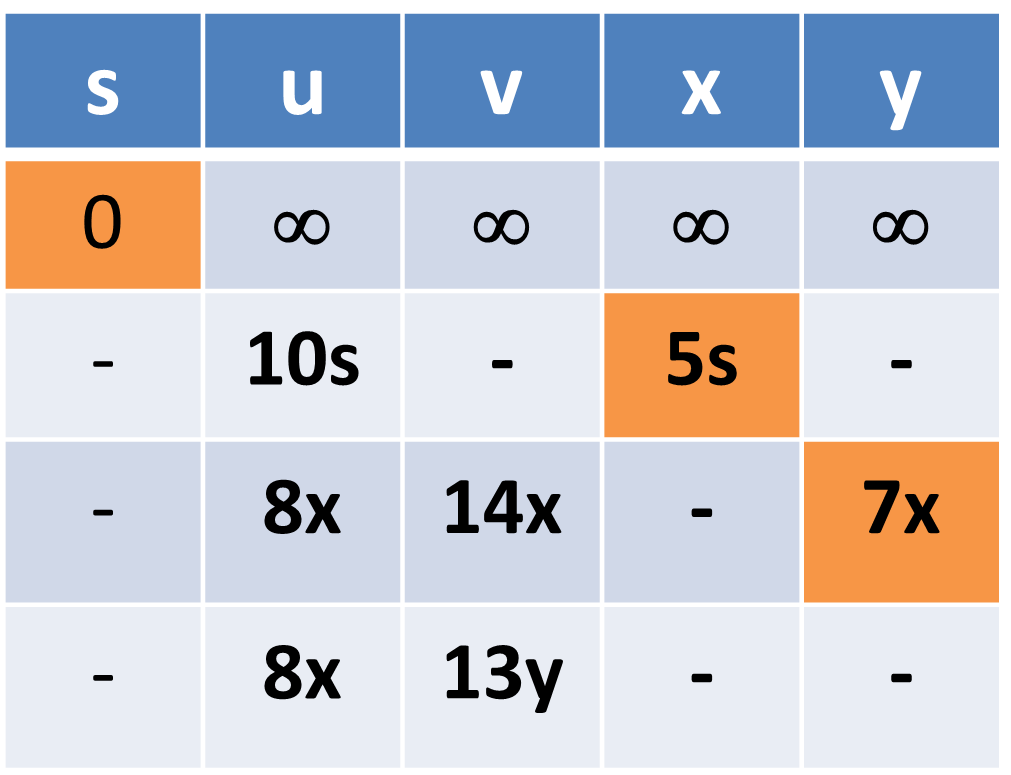
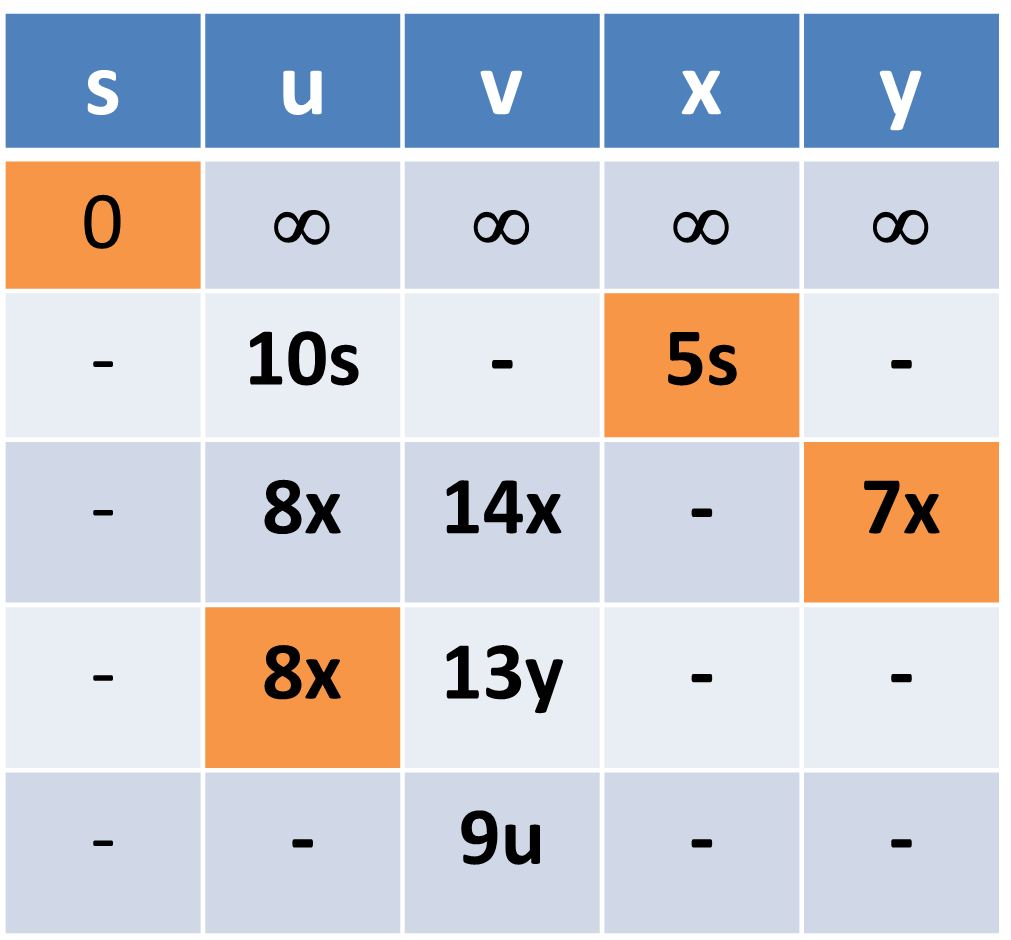
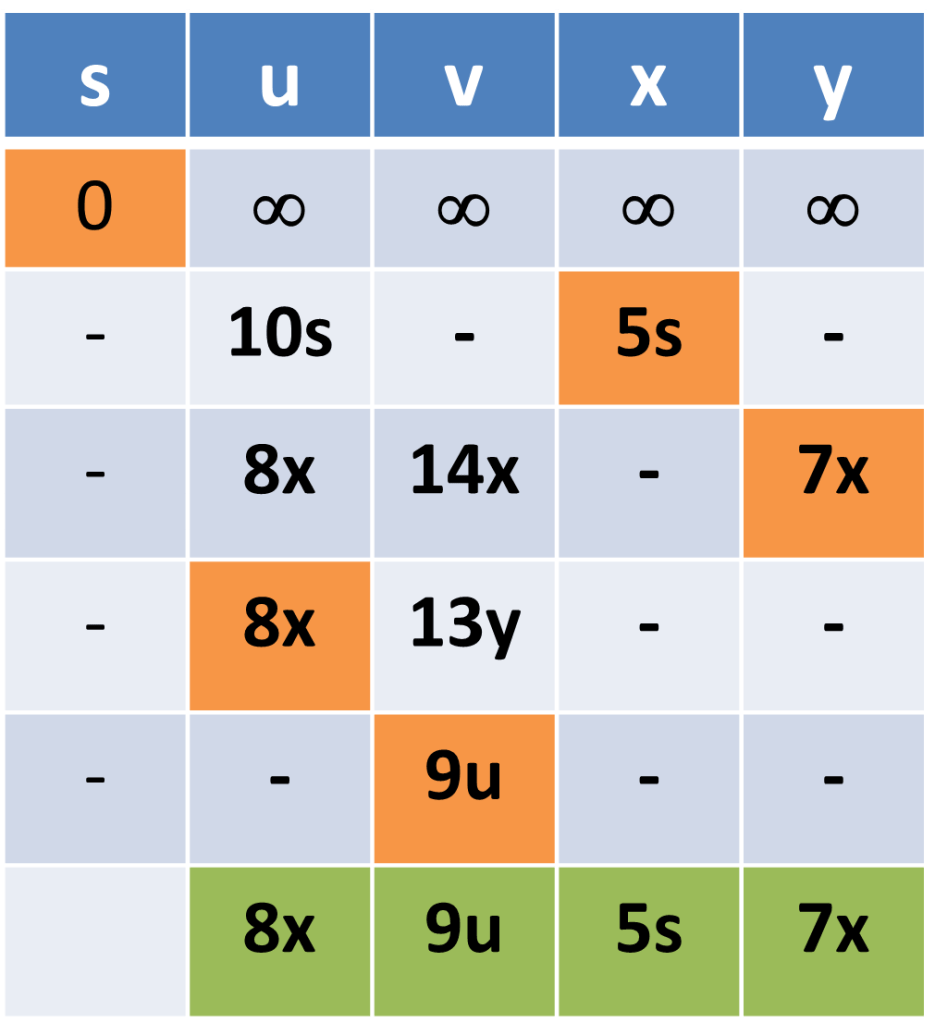
Question : Find shortest path from vertex S to all other nodes using Djikshtra Algorithms

Solution : Detailed iterations are shown as follows ( click for video explanation )

Final Answer

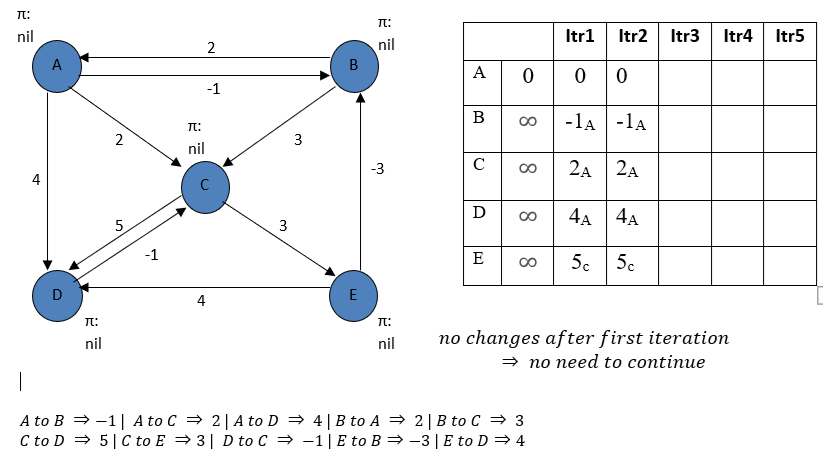
Question : Find shortest path from vertex A to all other nodes using Bellman Ford Algorithm

Solution : Detailed iterations are shown alogside ( click for video explanation )

Solving 0/1 Knapsack and Fractional Knapsack using Greedy Approach

Solve the following knapsack problem for following data values and knapsack capcity =60 kg

Item	I1	I2	I3	I4	I5
Weight(kg)	5	10	20	30	40
Value	30	20	100	90	160

Solution – First find the preciousness of each item to make decision (click for video explanation)

Item	val	Wt	Val/wt	Rank	Item Selected
I1	30	5	30/5 = 6	1	Yes
I2	20	10	20/10 =2	5	No
I3	100	20	100/20 = 5	2	Yes
I4	90	30	90/30 = 3	4	Yes
I5	160	40	160/40 = 4	3	No

Solving 0/1 Knapsack – Item selected based on rank (Greedy approach -select most precious item)

First Choice -Item 1 (5 kg) = > yes (capacity remaining = 60 – 5 = 55)

Second Choice -Item 3 (20 kg) = > yes (capacity remaining = 55 – 20 = 35)

Third Choice -Item 5 (40 kg) = > No (capacity remaining = 35)

Fourth Choice -Item 4 (30 kg) = > yes (capacity remaining = 35 – 30 = 5)

Fifth Choice -Item 2 (10 kg) = > No (capacity remaining = 5)

Total Gain attained by Items (val of I1+I3+I4) = 30+100+90 = 220

Note – this is NO optimal solution (optimal will be attained by selecting Item3 and Item5 (i.e. 100+160= 260), therefore, thus 0/1 Knapsack cannot be solved optimally using Greedy Method

Solving Fractional Knapsack – Item selected based on rank (select most precious item)

First Choice -Item 1 (5 kg) = > yes (capacity remaining = 60 – 5 = 55)

Second Choice -Item 3 (20 kg) = > yes (capacity remaining = 55 – 20 = 35)

Third Choice -Item 5 (40 kg) = > Yes (capacity remaining = 35, so take fraction of item i.e. 35 kg)

For Item5=> 40 kg has value 160, therefore 35 kg has value 140

Total Gain attained by Items (val of I1+I3+I5) = 30+100+140 = 270

Note – this is Optimal solution, thus Fractional Knapsack can be solved optimally using Greedy Method (optimal will be attained by selecting Item3 and Item5 (i.e. 100+160= 260)

Knapsack Problem using Dynamic Programming

Question : Solve the Knapsack Problem using Dynamic programming for following 3 items

Weight <2, 3, 4, 5> Value <3, 7, 2, 9> knapsack Capacity = 5 kg

Solution : The detailed solution is shown in table below ( click for video explanation )

Cost	Weight		1	2	3	4	5
		I0	0	0	0	0	0
3	2	I1	0	3	3	3	3
7	3	I2	0	3	7	7	10
2	4	I3	0	3	7	7	10
9	5	I4	0	3	7	7	10

Answer => Items identified = Item1 and Item 2, Maximum Gain = 10

String Matching problems

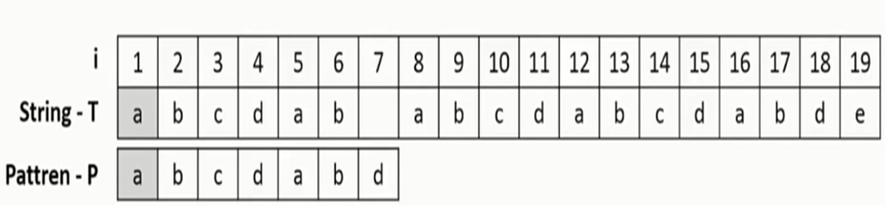
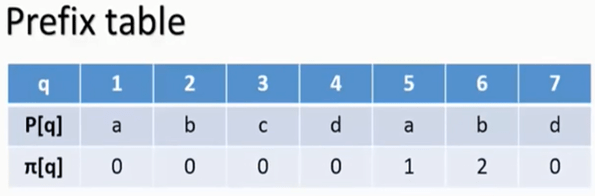
Ques : FInd the Pattern in the given Text using KMP algorithm

Solution – First find the Prefix table as follows (click for video explanation)

The shift made during the process is shown alongside. i is used to an index of Text, q is number of characters in Pattern found matched with Text, pi[q] refers to value in prefix table and will be used whenever mismatched is found. The Pattern is found in Text at 11th shift

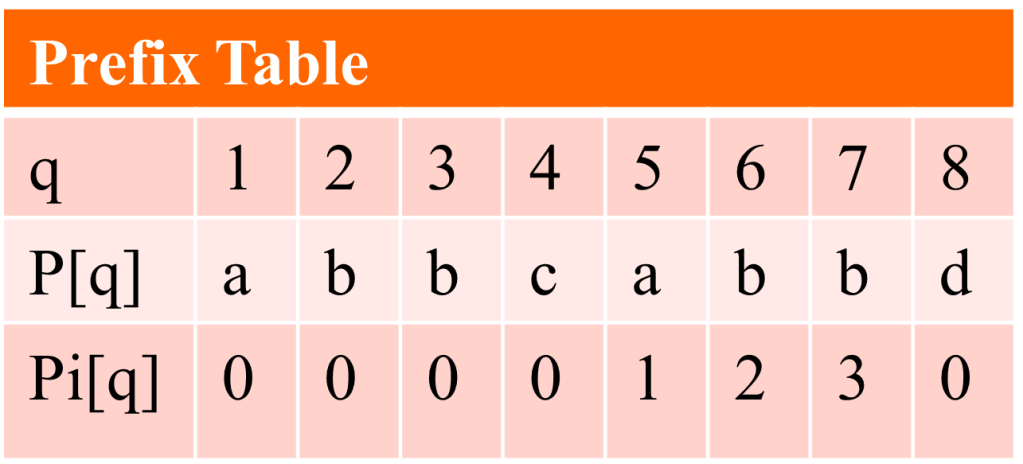
Note – Refer to KMP algorithm for the steps used in above table

Ques : FInd the Pattern in the given Text using KMP algorithm

Text : abbcabbccaabbcabbdde Pattern : abbcabbd

Solution – First find the Prefix table as follows

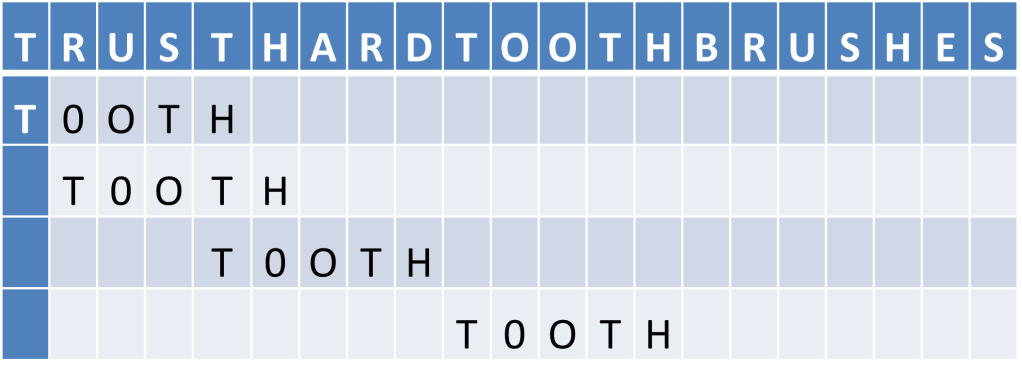
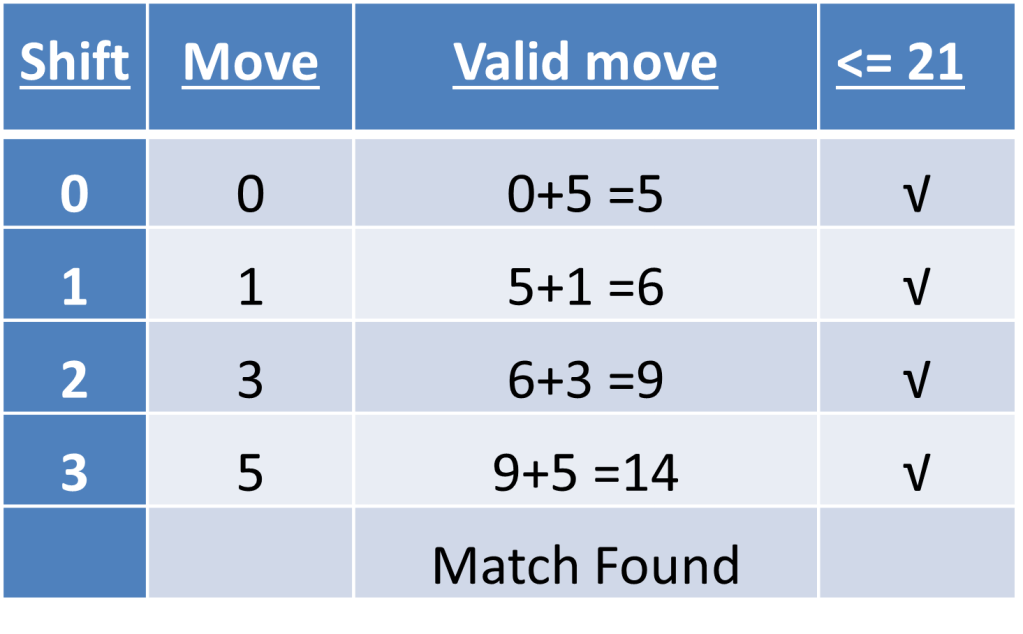
The shift made during the process is shown alongside.The Pattern is found in Text at 11th shift

Ques : FInd the Pattern in the given Text using Boyers Moore algorithm

Text : trusthardtoothbrushes Pattern : toothd

Solution – First find the Bad Match table as follows (click for video explanation)

Constructing Bad-Match table 
Value = length – index -1 ( index starts with 0)
Last letter = length , if not already defined
Every remaining letter (*) = length - i
Note:Shifting for cases would be used as (value – i), where i is the number of matched characters

Shift are shown as below

Share this: